عدد جرمی چیست؟ بررسی کامل و تاریخچه

در دنیای شگفت‌انگیز شیمی و فیزیک هسته‌ای، هویت و رفتار هر اتم به وسیله چند عدد بنیادین تعریف می‌شود. در میان این اعداد، عدد جرمی (Mass Number)، که با نمادA  نمایش داده می‌شود، نقشی محوری در شناسایی هسته اتم و درک پدیده‌هایی چون ایزوتوپ‌ها، پایداری هسته‌ای و واکنش‌های هسته‌ای ایفا می‌کند. این عدد ساده، که در نگاه اول ممکن است صرفاً یک شمارش به نظر برسد، در واقع کلیدی برای گشودن اسرار هسته اتم و منبع انرژی ستارگان است.

اما عدد جرمی دقیقاً چیست و چه چیزی را می‌شمارد؟ تاریخچه کشف آن چگونه با مدل‌های اتمی گره خورده است؟ تفاوت حیاتی آن با مفاهیم مشابهی مانند “عدد اتمی” و “جرم اتمی” در چیست؟ و چرا این عدد صحیح، سنگ بنای درک ما از تنوع عناصر در طبیعت و اساس فناوری‌های هسته‌ای مدرن است؟

این مقاله سفری جامع به مفهوم عدد جرمی است. ما از آزمایش‌های تاریخی که به کشف هسته و اجزای آن منجر شد آغاز می‌کنیم، به تعریف دقیق و نحوه نمایش آن می‌پردازیم، نقش آن در تعریف ایزوتوپ‌ها را کالبدشکافی کرده و اهمیت آن را در پدیده‌هایی از رادیواکتیویته گرفته تا شکافت و همجوشی هسته‌ای بررسی خواهیم کرد. با ما همراه باشید تا این مفهوم اساسی را به طور کامل درک کرده و جایگاه بی‌بدیل آن را در علوم مدرن کشف کنید.

تاریخچه: سفری به قلب اتم و کشف هسته

برای درک عدد جرمی، باید به زمانی بازگردیم که اتم دیگر یک کره صُلب و غیرقابل تقسیم (مانند مدل دالتون) نبود. داستان ما در اواخر قرن نوزدهم و اوایل قرن بیستم، با مجموعه‌ای از کشف‌های انقلابی آغاز می‌شود که دیدگاه ما را نسبت به ماده برای همیشه تغییر داد.

کشف الکترون و مدل کیک کشمشی

در سال ۱۸۹۷، جی. جی. تامسون (J. J. Thomson) با آزمایش روی لوله‌های پرتو کاتدی، ذره‌ای با بار منفی به نام الکترون را کشف کرد. از آنجایی که اتم در حالت کلی خنثی است، تامسون نتیجه گرفت که باید جرمی با بار مثبت نیز وجود داشته باشد تا بار منفی الکترون‌ها را خنثی کند. او مدل اتمی “کیک کشمشی” (Plum Pudding Model ) را پیشنهاد داد. در این مدل، اتم کره‌ای با بار مثبت پراکنده بود که الکترون‌های منفی مانند کشمش در آن فرو رفته بودند. در این مدل، هنوز خبری از یک هسته مرکزی و متمرکز نبود.

آزمایش ورقه طلا و تولد هسته

نقطه عطف واقعی در سال ۱۹۰۹ با آزمایش مشهور ارنست رادرفورد (Ernest Rutherford) و همکارانش، هانس گایگر و ارنست مارسدن، رقم خورد. آن‌ها باریکه‌ای از ذرات آلفا (هسته‌های هلیوم با بار مثبت) را به سمت یک ورقه بسیار نازک طلا شلیک کردند. بر اساس مدل تامسون، انتظار می‌رفت که تمام ذرات آلفا با انحرافی جزئی، مستقیماً از ورقه عبور کنند.

نتایج شگفت‌انگیز بود. اگرچه بیشتر ذرات طبق انتظار عبور کردند، اما تعداد بسیار کمی از آن‌ها با زوایای بسیار بزرگ منحرف شدند و حتی برخی تقریباً به سمت منبع بازگشتند! رادرفورد بعدها این تجربه را این‌گونه توصیف کرد: “مثل این بود که یک گلوله توپ ۱۵ اینچی را به سمت یک دستمال کاغذی شلیک کنید و گلوله به سمت خودتان بازگردد.”

این نتایج تنها یک تفسیر می‌توانست داشته باشد:

1. بیشتر حجم اتم فضای خالی است (دلیل عبور اکثر ذرات).
2. تقریباً تمام جرم اتم و کل بار مثبت آن در یک ناحیه بسیار کوچک، چگال و مرکزی به نام هسته (Nucleus) متمرکز شده است.

این کشف، مدل “سیاره‌ای” اتم را پایه‌گذاری کرد: یک هسته مثبت در مرکز و الکترون‌هایی که در مدارهایی به دور آن می‌چرخند.

کشف پروتون و نوترون

رادرفورد در ادامه تحقیقاتش، در سال ۱۹۱۹ ذره‌ای با بار مثبت را در هسته شناسایی و آن را پروتون (Proton) نامید. برای مدتی تصور می‌شد که هسته تنها از پروتون‌ها تشکیل شده است، اما این مدل نمی‌توانست جرم هسته‌ها را به درستی توضیح دهد. برای مثال، هسته هلیوم دو برابر بار مثبت هیدروژن را داشت (یعنی ۲ پروتون) اما جرم آن چهار برابر بود. این “جرم گمشده” یک معما بود.

پاسخ در سال ۱۹۳۲ توسط جیمز چادویک (James Chadwick)، یکی از شاگردان رادرفورد، پیدا شد. او با بمباران بریلیوم با ذرات آلفا، تابشی با قدرت نفوذ بالا و بدون بار الکتریکی را شناسایی کرد. او این ذره خنثی را نوترون (Neutron) نامید. نوترون جرمی تقریباً برابر با پروتون داشت.

با کشف نوترون، تصویر هسته کامل شد. هسته اتم از پروتون‌ها (با بار مثبت) و نوترون‌ها (بدون بار) تشکیل شده است. این ذرات مجموعاً نوکلئون (Nucleon) نامیده می‌شوند. و اینجاست که به تعریف دقیق عدد جرمی می‌رسیم.

عدد جرمی (A) چیست؟ تعریف دقیق

عدد جرمی  (Mass Number)، که با نماد A نمایش داده می‌شود، برابر است با مجموع تعداد پروتون‌ها و نوترون‌ها در هسته یک اتم.

A=(تعداد پروتون‌ها)+(تعداد نوترون‌ها)

A=Z+N

در این رابطه:

• A  نماد عدد جرمی است.
• Z  نماد عدد اتمی (تعداد پروتون‌ها) است.
• N  نماد تعداد نوترون‌ها است.

نکات کلیدی درباره عدد جرمی:

1. همیشه یک عدد صحیح است: از آنجایی که عدد جرمی حاصل شمارش تعداد نوکلئون‌هاست، هرگز نمی‌تواند یک عدد کسری یا اعشاری باشد.
2. جرم را تخمین می‌زند، نه اندازه‌گیری: عدد جرمی به ما یک تخمین خوب از جرم کل هسته بر حسب “واحد جرم اتمی (amu)” می‌دهد، زیرا جرم هر پروتون و هر نوترون تقریباً برابر با ۱ amu است. به همین دلیل نام آن “عدد جرمی” است. اما این عدد با “جرم اتمی” واقعی که یک مقدار اندازه‌گیری شده و اعشاری است، تفاوت دارد.
3. هویت هسته را مشخص می‌کند: عدد جرمی به همراه عدد اتمی، یک ایزوتوپ خاص را به طور کامل تعریف می‌کند.

تمایز حیاتی: عدد جرمی در مقابل عدد اتمی و جرم اتمی

درک تفاوت این سه مفهوم برای هر دانش‌پژوه شیمی و فیزیک ضروری است. این مفاهیم اغلب با هم اشتباه گرفته می‌شوند، اما هر یک جنبه متفاوتی از اتم را توصیف می‌کنند.

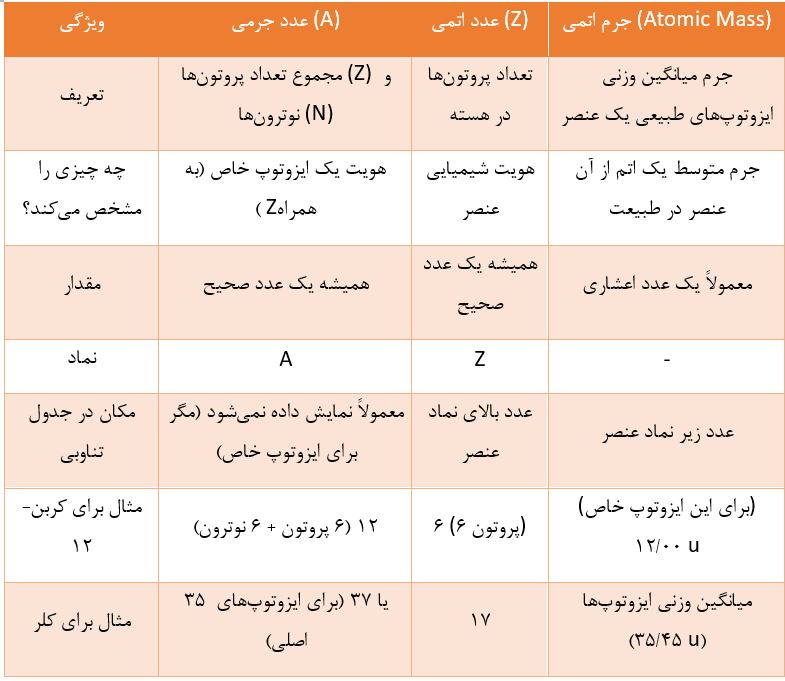
به طور خلاصه:

• عدد اتمی (Z) به شما می‌گوید اتم متعلق به کدام عنصر است (مثلاً هر اتمی با ۶ پروتون، کربن است).
• عدد جرمی (A) به شما می‌گوید با کدام نسخه یا ایزوتوپ از آن عنصر سر و کار دارید (مثلاً کربن-۱۲ یا کربن-۱۴).
• جرم اتمی به شما می‌گوید وزن متوسط اتم‌های آن عنصر در یک نمونه طبیعی چقدر است.

ایزوتوپ‌ها: خانواده‌ای از اتم‌ها با یک نام

اکنون که عدد جرمی را می‌شناسیم، می‌توانیم به سادگی مفهوم ایزوتوپ (Isotope) را تعریف کنیم. ایزوتوپ‌ها اتم‌هایی هستند که:

• عدد اتمی (Z) یکسانی دارند (یعنی تعداد پروتون‌هایشان برابر است.)
• عدد جرمی (A) متفاوتی دارند (یعنی تعداد نوترون‌هایشان متفاوت است.)

از آنجایی که خواص شیمیایی یک عنصر عمدتاً توسط تعداد الکترون‌ها تعیین می‌شود (که برابر با تعداد پروتون‌ها در اتم خنثی است)، ایزوتوپ‌های یک عنصر خواص شیمیایی تقریباً یکسانی دارند و در جدول تناوبی در یک خانه قرار می‌گیرند. (کلمه ایزوتوپ از ریشه یونانی “iso-topos” به معنای “همان مکان” گرفته شده است.)

مثال: ایزوتوپ‌های هیدروژن هیدروژن، ساده‌ترین عنصر، سه ایزوتوپ معروف دارد:

1. پروتیوم (هیدروژن معمولی): ۱ پروتون، ۰ نوترون. (A=1,Z=1)
2. دوتریوم (هیدروژن سنگین): ۱ پروتون، ۱ نوترون. (A=2,Z=1)
3. تریتیوم (هیدروژن رادیواکتیو): ۱ پروتون، ۲ نوترون. (A=3,Z=1)

هر سه، هیدروژن هستند و با اکسیژن ترکیب شده و آب (H_۲​O,D_۲​O,T_۲​O) تولید می‌کنند، اما به دلیل تفاوت در عدد جرمی، خواص فیزیکی متفاوتی (مانند چگالی و نقطه جوش) و پایداری هسته‌ای متفاوتی دارند.

نمادگذاری ایزوتوپ‌ها

برای نمایش یک ایزوتوپ خاص، از نماد AZX یا نماد نوکلید (Nuclide) استفاده می‌شود:

• X  نماد شیمیایی عنصر است.
• A  عدد جرمی است که به صورت بالانویس در سمت چپ نماد نوشته می‌شود.
•  Z عدد اتمی است که به صورت زیرنویس در سمت چپ نماد نوشته می‌شود.

مثال‌ها:

• کربن-۱۲: _۶^۱۲​C
• اورانیوم-۲۳۵: _۹۲^۲۳۵​U

گاهی اوقات برای سادگی، عدد اتمی (Z) حذف می‌شود، زیرا نماد عنصر (X) خود گویای آن است.

عدد جرمی و پایداری هسته: نقش نوترون‌ها

چرا هسته اتم با وجود نیروی دافعه الکترواستاتیکی شدید بین پروتون‌های مثبت، از هم نمی‌پاشد؟ پاسخ در نیروی هسته‌ای قوی نهفته است؛ یک نیروی جاذبه بسیار قدرتمند اما کوتاه‌برد که بین تمام نوکلئون‌ها (پروتون-پروتون، نوترون-نوترون و پروتون-نوترون) عمل می‌کند.

نوترون‌ها در این میان نقشی حیاتی به عنوان “چسب هسته‌ای” ایفا می‌کنند. آن‌ها بدون افزودن به دافعه الکترواستاتیکی، به نیروی جاذبه هسته‌ای قوی می‌افزایند و به پایداری هسته کمک می‌کنند.

رابطه بین تعداد پروتون‌ها (Z) و نوترون‌ها (N) برای پایداری هسته بسیار مهم است:

• برای عناصر سبک (Z < 20): پایدارترین ایزوتوپ‌ها آن‌هایی هستند که نسبت نوترون به پروتون (N/Z) در آن‌ها تقریباً برابر با ۱ است.
• برای عناصر سنگین (Z > 20): با افزایش تعداد پروتون‌ها، دافعه الکترواستاتیکی به شدت زیاد می‌شود. برای غلبه بر این دافعه، به تعداد بیشتری نوترون نیاز است. بنابراین، نسبت N/Z  در هسته‌های سنگین پایدار به تدریج افزایش یافته و به حدود ۵/۱ می‌رسد.

هسته‌هایی که از این “کمربند پایداری” خارج شوند، ناپایدار بوده و از طریق واپاشی رادیواکتیو تلاش می‌کنند تا با تغییر تعداد پروتون‌ها و نوترون‌های خود، به یک حالت پایدارتر برسند. در این واپاشی‌ها، عدد جرمی می‌تواند تغییر کند یا ثابت بماند.

قانون بقای عدد جرمی در واکنش‌های هسته‌ای

یکی از اصول بنیادین در فیزیک هسته‌ای، قانون بقای عدد جرمی (Conservation of Mass Number) است. این قانون بیان می‌کند که:

“در یک واکنش هسته‌ای، مجموع اعداد جرمی واکنش‌دهنده‌ها برابر با مجموع اعداد جرمی محصولات است.”

این قانون، به همراه قانون بقای بار (عدد اتمی)، ابزاری قدرتمند برای موازنه و پیش‌بینی محصولات واکنش‌های هسته‌ای است.

مثال: واپاشی آلفا

در واپاشی آلفا، یک هسته ناپایدار یک ذره آلفا (_۲^۴​He) از خود گسیل می‌کند. برای مثال، واپاشی اورانیوم-۲۳۸

_۹۲^۲۳۸​U→_۹۰^۲۳۴​Th+_۲^۴​He

موازنه عدد جرمی: ۲۳۸=۲۳۴+۴ (برقرار است) موازنه عدد اتمی   : 92=90+2 (برقرار است)

مثال: شکافت هسته‌ای (Nuclear Fission)

در فرآیند شکافت، یک هسته سنگین مانند اورانیوم-۲۳۵ با جذب یک نوترون، به دو هسته سبک‌تر، چند نوترون و مقدار عظیمی انرژی تجزیه می‌شود:

_۹۲^۲۳۵​U+​n→_۵۶^۱۴۱​Ba+_۳۶^۹۲​Kr+3​n

موازنه عدد جرمی: ۲۳۵+۱=۱۴۱+۹۲+(۳×۱)⇒۲۳۶=۲۳۶ (برقرار است)

این قانون در تمام فرآیندهای هسته‌ای، از جمله همجوشی هسته‌ای (Nuclear Fusion) که در آن هسته‌های سبک به هم جوش خورده و هسته‌های سنگین‌تر می‌سازند، نیز صادق است.

کاربردها و اهمیت عدد جرمی در علوم مدرن

عدد جرمی فراتر از یک مفهوم تئوریک، در بسیاری از زمینه‌های علمی و فناوری کاربردهای حیاتی دارد:

• پزشکی هسته‌ای: ایزوتوپ‌های رادیواکتیو (رادیوایزوتوپ‌ها) که با عدد جرمی خاص خود شناخته می‌شوند، در تشخیص (مانند PET scan با استفاده از فلوئور-۱۸) و درمان بیماری‌ها (مانند پرتودرمانی با کبالت-۶۰) استفاده می‌شوند.
• انرژی هسته‌ای: کنترل واکنش‌های زنجیره‌ای شکافت در ایزوتوپ‌هایی مانند اورانیوم-۲۳۵ (A=235) اساس کار نیروگاه‌های هسته‌ای برای تولید برق است.
• تاریخ‌نگاری و باستان‌شناسی: روش سن‌سنجی رادیوکربن با اندازه‌گیری نسبت ایزوتوپ ناپایدار کربن-۱۴ (A=14)  به ایزوتوپ پایدار کربن-۱۲ (A=12)، قدمت مواد آلی را تا ده‌ها هزار سال تخمین می‌زند.
• شیمی تجزیه و طیف‌سنجی جرمی: در دستگاه طیف‌سنج جرمی، یون‌ها بر اساس نسبت جرم به بار جداسازی می‌شوند. این دستگاه قادر است ایزوتوپ‌های مختلف یک عنصر را بر اساس تفاوت در عدد جرمی آن‌ها از هم تفکیک کرده و فراوانی هر یک را مشخص کند.
• ژئوشیمی و علوم محیطی: نسبت ایزوتوپ‌های پایدار عناصر (که با عدد جرمی‌شان متمایز می‌شوند) مانند اکسیژن (18O  به 16O)  در نمونه‌های یخ و رسوبات، اطلاعات ارزشمندی درباره تغییرات آب و هوای گذشته زمین به دست می‌دهد.

نتیجه‌گیری: عدد جرمی، شناسنامه هسته اتم

عدد جرمی، در عین سادگی تعریفش به عنوان مجموع پروتون‌ها و نوترون‌ها، مفهومی عمیق و قدرتمند است که از دل تاریخ پر فراز و نشیب کشف ساختار اتم بیرون آمده است. این عدد، شناسنامه هر هسته اتمی است که نه تنها هویت یک ایزوتوپ خاص را مشخص می‌کند، بلکه سرنخ‌های مهمی درباره پایداری، رفتار هسته‌ای و نقش آن در طبیعت به ما می‌دهد.

از تعریف خانواده عناصر در قالب ایزوتوپ‌ها گرفته تا موازنه واکنش‌هایی که انرژی خورشید را تأمین می‌کنند و اساس کار نیروگاه‌های هسته‌ای را تشکیل می‌دهند، عدد جرمی حضوری همیشگی و تعیین‌کننده دارد. درک دقیق تفاوت آن با عدد اتمی و جرم اتمی، یک ضرورت برای ورود به دنیای مدرن شیمی و فیزیک است. در نهایت، عدد جرمی به ما یادآوری می‌کند که در قلب هر اتم، دنیایی از قوانین دقیق و شگفت‌انگیز حاکم است که شمارش ساده نوکلئون‌ها، اولین گام برای ورود به آن است.